The tuning of Proportional-Integral-Derivative (PID) can be considered a mix of art and science. It's an art where one needs to use their judgment and experience to understand the controller’s behavior. The science of tuning comes into the picture where one uses open-loop mathematical models and different techniques to derive the tuning parameters. The “Art” of tuning helps to understand the how’s and why’s of the process, and the “Science” of tuning provides a roadmap for tuning.
The performance of any PID controller depends on tuning parameters, i.e., gain, integral time, and derivative time that is set in. The tuning parameters are a function of process types, functionality expected from the PID loop, i.e., variance reduction or setpoint tracking, and type of the PID loop.
PID Tuning methods
The PID controller combines the proportional, integral, and derivative action on the error and converts it into controller output. The ISA algorithm for PID controller is as follows:

The different methods of PID tuning are as follows:
- Trial and Error method
- Feature-based method (Ziegler-Nichols method, Cohen-Coon method)
- Model-based PID tuning.
Trial and Error Method
The trial-and-error method is one of the basic methods for PID tuning and depends on the PID controller's visual inspection. However, it doesn't guarantee success and consumes too much time. Hence, it is not an ideal choice for process control engineers.
Ziegler-Nichols method
The Ziegler-Nichols (ZN) method provides a set of tuning rules for PID tuning. These tuning rules were obtained by carrying out extensive experiments on different types of processes. The process is assumed to be first-order while using these rules. To use this method, the plant’s open-loop step response should be in the following shape:
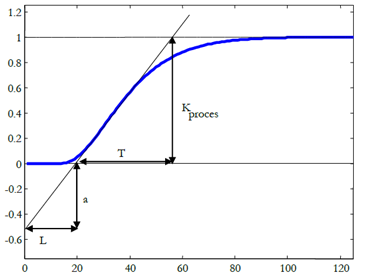
Three parameters characterize the process: the steady-state gain Kprocess, the time delay L, and the time constant T. Here, ‘a’ is calculated as a = (Kprocess * L) / T. Once these parameters are calculated based on process response, the tuning parameters are selected from the table below:
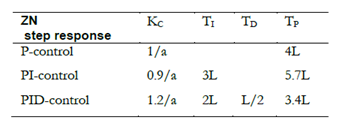
The ZN method is simple and requires less process knowledge. Still, there are disadvantages associated with it, such as the assumption of the process to be linear, High proportional gain due to 25% overdesign consideration, and works well for operations with large time constants relative to deadtime.
Cohen-Coon method
The Cohen-Coon (CC) method is a modification of the ZN method. The additional parameter calculated in this method is ‘τ’, τ = L/(L+T).
Once these parameters are calculated based on process response, the tuning parameters are selected from the table below:

The Cohen-Coon method provides good results for tuning self-regulating processes, but it does not perform well for integrating processes.
The methods discussed above provide good tuning results for a simple controller, but there are limitations associated with each method. Also, these methods offer too low robustness against changes in the process dynamics and when it comes to tuning of complex PID loops, getting tuning parameters right for the first time is important. In the following section, the advantages of model-based PID tuning over heuristic methods and the ability of INCA Aptitune to provide robust tuning results are discussed.
Model-based PID tuning
The model-based PID tuning works on the principle that the PID controller's open-loop Model is identified, and the tuning parameters are calculated based on these models. INCA Aptitune is software that identifies the Model and calculates the tuning parameters for the PID controller.
One can avoid the time-consuming ZN and CC tuning rules and use model-based PID tuning feature of INCA Aptitune. INCA Aptitune helps to get the optimal tuning parameters right at the first time and at the same time make the PID loop robust against process changes.
Traditional tuning techniques vs. Model-based PID tuning
A comparison of PID tuning parameters obtained for a PID controller with Process gain (Kprocess) =1, Deadtime (L) =5, and Settling time (T) =10 using the traditional method and INCA Aptitune is shown below:
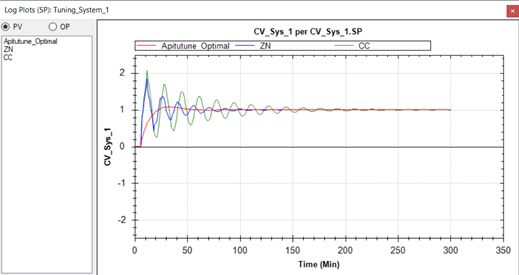
As can be seen in the image above, the tuning parameters obtained using ZN and CC method causes PID loop to oscillate. Thus, additional time will be required to fine tune the tuning obtained by these methods, but the INCA Aptitune will give optimal tuning parameters at one shot. The tuning parameters obtained are:
|
Tuning Method |
Proportional gain |
Integral time (min) |
Derivative time (min) |
|
Ziegler-Nichols |
2.4 |
10 |
2.5 |
|
Cohen-Coon |
2.94 |
10.54 |
1.68 |
|
INCA Aptitune |
0.82 |
7.52 |
2.14 |
The tuning of the PID controller can be a headache for complex loops using traditional techniques. The model-based PID tuning is a quick and reliable technique, and it also saves a lot of time. INCA Aptitune has a simple workflow and provides robust tuning parameters that will bring stability to a process plant.
INCA Aptitune has custom-made templates available for different DCS vendors that help select appropriate algorithms specific to a DCS.
More information?
Do you want to learn more about the INCA Aptitune tuning software, learn more about how it stabilizes your plant, and reduces alarms and operator interventions? Request a 30-minute live demo and gain insights into what you can achieve with INCA Tools PID Tuning. It is all you need to get your PID controllers’ tuning right the first time.




